BAS KUNSTLER REKENT
VAN PAPYRUS TOT COMPUTER
Bas Kunstler rekent. Van papyrus tot computer
Eén thema uit de wiskunde, de binaire code, leidt tot boeiende rekenopgaven voor 4e, 5e en 6e leerjaar, waarbij de kinderen kennismaken met verhalen, historische figuren, genealogie en tal van interessante feiten en oefeningen uit de geschiedenis van de wiskunde.
124 bladzijden
FSC-papier van 90 gram.
Talrijke illustraties, zwart/wit + kleur
Oefeningen
15,00 euro
Bekijk hieronder een aantal bladzijden uit het boek.
Klik op de pagina's voor een grotere afbeelding.
Het rekensysteem van de oude Egyptenaren vind je terug in de hedendaagse computers. In de lagere school kun je een reeks rekenopgaven aanbieden aan leerlingen van het vierde tot en met het zesde leerjaar waarin zij de evolutie van het Egyptische rekenen tot de manier waarop de computer met cijfers en getallen omgaat, ontdekken en meemaken.
Geschiedenis, aardrijkskunde, cultuurbeschouwing, vreemde talen, tekenen, meetkunde, hoofdrekenen, cijferen, actualiteit, fysica, akoestiek, muziek, verhalen, lezen, anatomie, biologie, genealogie, filosofie, ICT, kalligrafie en handvaardigheid komen allemaal samen in dit ene onderwerp: hoe de rekenkunde van het Oude Egypte aan de basis ligt van de huidige digitale wereld.
----------------------
Aanvullingen bij het boek Bas Kunstler rekent. Van papyrus tot computer.
Wetenschapskalender 2022 stelt op 19 augustus deze vraag:
Vijf dalmatiërs
In wat voor wereld heb je het over vijf dalmatiërs, sprookjes van negen nachten en het tv-programma één tegen vier?
Hmm…
Op de verso-zijde staat het antwoord :
Dat is een wereld waarin we een binair getallenstelsel zouden gebruiken. In binaire getallen staat het cijfer 101 immers gelijk aan het getal vijf. Verder is 1001 gelijk aan negen en 100 gelijk aan vier. En 1 is gewoon één.
Hoe reken je zo’n binair getal om naar ons tientallig stelsel? Doe het meest rechter cijfer van het binaire getal maal één, het cijfer links daarvan maal twee, het cijfer daarnaast maal vier, dat daarnaast maal acht enzovoort. Tel de resulterende getallen bij elkaar op.
Een binaire 1001 is dus gelijk aan een tientallige 1 x 1 + 0 x 2 + o x 4 + 1 x 8 = 9. En een binaire 100 is een tientallige 0 x 1 + 0 x 2 + 1 x 4 = 4.
Het woord cijfer wordt in deze tekst zowel voor een getal als een cijfer gebruikt, wat verwarrend is.
101 is een getal dat uit drie cijfers bestaat en niet een cijfer dat uit drie cijfers bestaat.
DE BINAIRE GETALLEN IN DE COMBINATIEDRIEHOEK VAN PASCAL.
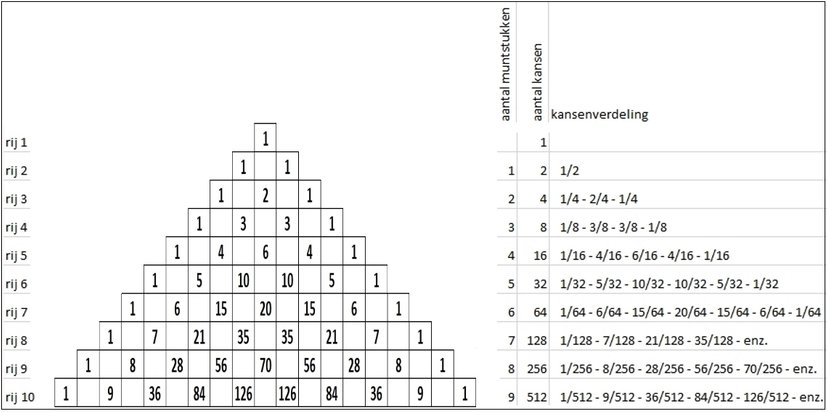
Deze tekst is opgenomen in de nieuwe druk, augustus 2022De binaire getallen die je verkrijgt door de rijen horizontaal op te tellen, geven het aantal mogelijkheden weer die je hebt bij kansspelen, bijvoorbeeld bij het tossen.
Hoeveel kansen heb je om met een geldstuk kop of munt te gooien? Met één muntstuk heb je 1 kans op 2 om kruis of munt te gooien. In de tweede rij van de combinatiedriehoek zie je het getal 1 staan. Deze 1 staat voor 1 muntstuk. De som van de rij is 2: dit zijn de 2 mogelijkheden (kansen).
Het tweede getal van elke rij geeft het aantal geldstukken weer.
De som van de rij geeft het aantal kansen aan.
In de derde rij heb je de getallen 1 - 2 - 1.
2 verwijst naar 2 muntstukken.
De som van 1 - 2 - 1 is 4: dit zijn de 4 kansen (mogelijkheden).
De kans dat je tweemaal kruis gooit is 1 op 4.
De kans dat je éénmaal kruis en éénmaal munt gooit is 2 op 4.
De kans dat je tweemaal munt gooit is 1 op 4.
Op de vierde rij heb je de getallen 1 - 3 - 3 - 1.
3: het gaat om 3 muntstukken.
De som van de rij is 8. Je hebt dus 8 kansen.
Je hebt 1 kans op 8 dat je driemaal kruis gooit (= 1 op 8 of 1/8).
Je hebt 3 kansen op 8 dat je tweemaal kruis en éénmaal munt gooit (= 3 op 8 of 3/8).
Je hebt 3 kansen op 8 dat je tweemaal munt en éénmaal kruis gooit (= 3 op 8 of 3/8).
Je hebt 1 kans op 8 om driemaal munt te gooien (= 1 op 8 of 1/8).
Op de vijfde rij heb je de getallen 1 - 4 - 6 - 4 - 1.
4 muntstukken. Som van de rij is 16.
4 x kruis = 1 op 16
3 x kruis + 1 x munt = 4 op 16 (= 1 op 4 of 1/4)
2 x kruis + 2 x munt = 6 op 16 (= 1,5 op 4)
1 x kruis + 3 x munt = 4 op 16 (= 1 op 4 of 1/4)
4 x munt = 1 op 16.
---------------------
NAWOORD
Met dit éne onderwerp: de binaire getallen, kun je in de lagere school een uitgebreid gamma aan lesinhouden ontwikkelen. Een overzicht van wat in dit boek aan bod kwam:
Hoofdrekenen
Cijferen
Getalkennis en – kwaliteit
Talstelsels
Geschiedenis
Aardrijkskunde
Verhalen
Anatomie
Genealogie
Filosofie
ICT (zowel hardware als software)
Muziek
Akoestiek (fysica)
Tekenen
Meetkunde
Biologie
Kalligrafie
Engels
Frans
Latijn
Grieks
Cultuur
Economie
Handvaardigheid
--------------
Het gebruik van de computer op school (lagere school)
Kinderen zijn nog altijd het meest gedreven om te leren als de leerstof persoonlijk door de leerkracht verwerkt is en door hem/haar aangeboden wordt op een levendige en kunstzinnige manier. Als kinderen naast het gebruik van de computer ook inzicht verwerven in de werking van het toestel op een manier zoals dit bij wijze van voorbeeld in dit boek is beschreven, is er geen enkele reden om de computer niet als hulpmiddel in het leerproces te gebruiken.
In de kleuterschool
Ik ben absoluut geen voorstander van het gebruik van computers in de kleuterschool. Er is zo veel te beleven voor de kleuters, er zijn zo veel activiteiten waarin ze zich met hart en ziel kunnen geven, dat het niet nodig is om daarbovenop nog computers te gebruiken.
In de lagere school
Ik heb geen bezwaar tegen het gebruik van de computer in de lagere school. Maar ik koppelde er voor mezelf de voorwaarde aan dat de kinderen in de loop van de lagere school inzicht zouden krijgen in de werking van deze machine. In de geschiedenislessen over Egypte vond ik een geschikt aanknopingspunt. Het rekensysteem van de Egyptenaren was in grote lijnen een binair systeem (niet helemaal, want ze gebruikten ook een vorm van decimaal talstelsel). Dit was de link met de computer en het digitale stelsel dat nu niet meer weg te denken is uit ons leven.
Inzicht begint met de vraag: Wat doet een computer eigenlijk?
Computer is een woord dat afgeleid is van het Engelse werkwoord compute, dat uitrekenen betekent. Een computer is dus een rekentoestel. De digitale rekentoestellen doen dus eigenlijk perfect wat van hen verwacht wordt.
Met een computer kun je meer dan rekenen: je kunt hem zo programmeren dat hij niet meer rekent. Je kunt hem beletten te rekenen. Door bepaalde (binaire) getallen te verbinden met letters, kun je de cijfers vervangen door woorden. Je kunt de binaire getallen ook vervangen door tekens: rechte lijn, hoek, punt, leesteken, kleur, klank enz. In hoofdstuk 13 leren de kinderen hoe een byte (8 cijfers) een letter kunnen voorstellen. Een tekstverwerker is in feite niets anders dan een programma dat aan de computer vertelt dat hij niet mag rekenen en hem verplicht om de cijfers te vervangen door letters, Arabische cijfers, streepjes, punten, uitroeptekens, vraagtekens, spaties en zo meer. Elk softwareprogramma bevat aanwijzingen voor de computer om iets anders met de cijfers 1 en 0 te doen dan waarvoor ze oorspronkelijk gebruikt werden. Wat de kinderen in de vijfde klas leren met de ascii-code geeft hen inzicht in de functie van een softwarepakket zoals een tekstverwerker.
Als dat inzicht er is, en de kinderen ook ervaren hebben hoe de computer zelf rekent met de cijfers 1 en 0 (zoals in hoofdstukken 8 tot en met 11), kunnen ze de eerste stappen zetten in het programmeren om nog meer inzicht te verwerven in de functies van de computer. Met eenvoudige programma's om te leren progammeren, zoals Coderdojo, kunnen ze wat experimenteren.
In de loop van de lagere school - vanaf de eerste klas - liet ik de kinderen dagelijks een korte tijd werken met Shipdata (in het DOS-tijdperk) en later met Teach2000. Met deze software konden de kinderen zelf overhooroefeningen maken en konden ze zichzelf een oefenschema opleggen. Deze software gebruikten ze vooral voor rekenen, Frans, Engels, spelling, aardrijkskunde.
De dagelijkse opstellen (eigen teksten) konden de kinderen overtikken in Word (of Wordperfect) en printen, waarna ze deze teksten konden voorlezen.
Encarta en later Wikipedia liet ik gebruiken om aanvullende informatie op te zoeken bij vakken als aardrijkskunde, geschiedenis, fysica, astronomie enz.
Omdat mijn pedagogische werkwijze gebaseerd is op zelfwerkzaamheid van de leerlingen met veel schrijven, tekenen, schilderen, muziek, theater en véél beweging en samenwerking, kon de computer in de klas alleen een ondergeschikte en aanvullende rol spelen.
----
Augustus 2022: Ieder kind vanaf het vijfde leerjaar een computer geven op school, zoals de Vlaamse minister Weyts nu beslist heeft, lijkt me geen goed idee. Dat de kinderen een computer gebruiken voor bepaalde oefeningen en dat ze zelf leren oefeningen ontwerpen is een pluspunt. Ook informatie opzoeken is zinvol. Maar er zijn schaduwzijden aan het geven van een laptop aan ieder kind en ik stel me ook enkele vragen:
Het sociale aspect verdwijnt. Het wordt eens te meer ieder voor zich. Als er per klas een vier- of vijftal laptops ter beschikking zijn, is dat voldoende voor twintig kinderen. Zo kunnen ze ook op de computer samenwerken.
Kinderen moeten vooral schrijven met de hand. Het gevaar is dat ze, als ze over een eigen laptop beschikken, onmiddellijk op de computer werken en niet meer met de hand schrijven.
De laptops zullen vooral gebruikt worden om invuloefeningen te maken en informatie op te zoeken. Het zélf schrijven en het verwerven van parate kennis zal dus weer minder aangesproken worden, want men moet niet onthouden omdat alle info toch op te zoeken is.
De overheid legt verkeerde prioriteiten. Laptops financieren is geld weggooien. Men zou beter investeren in een degelijke lerarenopleiding, in leerkrachten die weten hoe ze alle talenten van kinderen kunnen ontwikkelen, dus ook de kunstzinnige.
Als de kinderen naar de middelbare school gaan zullen ze (hoogstwaarschijnlijk) een nieuwe laptop nodig hebben. Wat gebeurt er dan met de laptop die ze in de lagere school hadden? De afvalberg zal waarschijnlijk groter worden.
Zal men de kinderen ook leren hoe een computer rekent en zullen ze inzicht krijgen in de werking van een computer?
Als men de kinderen leert programmeren, kan ik me inbeelden dat je meer dan vier of vijf computers per klas nodig hebt, maar zelfs dan is het niet nodig om ieder kind een eigen laptop te geven. Bij leren programmeren is het zinvol om samen te werken aan één toestel. Maar zijn er lagereschoolklassen waar kinderen leren programmeren? Hier en daar wellicht wel, hoop ik.