|
https://www.cielen.eu |
|
MEETKUNDE VIJFDE KLAS Luc Cielen Terug naar https://cielen.eu/home/bas-kunstler-rekent/ of |
|
MEETKUNDE 5e klas 2020-2021 Maak
elke meetkundetekening met een hard, vlijmscherp potlood HB2 en druk er niet
te hard op. De maten schrijf je met potlood of fijne stift naast de lijnen.
De tekeningen werk je ten slotte af met kleurpotlood. Werk nooit uit de losse
hand, maar gebruik altijd lat, passer en tekendriehoek. Blad 1: Rechte lijnen
tekenen van bepaalde lengte kriskras op het blad, maar de lijnen mogen elkaar
niet snijden. Bij elke lijn de lengte in cm noteren. Onderaan op het blad de
totale lengte van alle lijnen samen noteren in cm, mm en m. Lengtes in cm
opgeven, enkele ook met komma (bv. 6,3 cm)
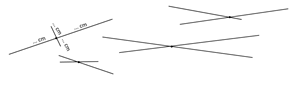
Blad 2: Rechte lijnen van
bepaalde lengte kriskras op het blad tekenen. De lijnen snijden elkaar per
twee. Noteer naast elk lijnstuk de lengte in cm. Onderaan op het blad de
totale som van alle lijnen noteren in cm, mm en m. Geef de lengtes op in cm,
enkele ook met komma.
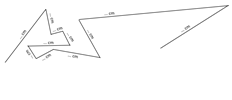
Blad 3: Teken een
gebroken lijn willekeurig over het blad. Meet elk lijnstuk van hoek tot hoek
in cm. Noteer onderaan het blad de som van alle lijnstukken in cm, mm en m.
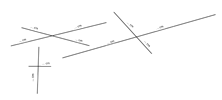
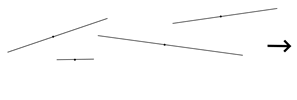
Blad 4: Teken lijnen
volgens opgegeven maten. Zoek het midden van elke lijn en teken een rechte
lijn die door dat punt gaat en de lijn snijdt. Geef de maten op in dm en cm,
enkele ook met een even cijfer achter de komma (bv. 12,6 cm – 2,6 dm).
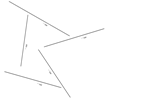
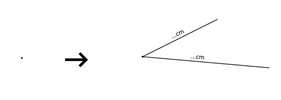
Blad 5: Zet een stip
ergens op het blad. Teken vanuit dat stip twee rechte lijnen die op die stip
een hoek maken. Zorg dat de hoeken allemaal verschillend zijn. Meet de lengte
van elke lijn in cm en schrijf die ernaast. De lijnen eerst tekenen, dan pas
meten.
Blad 6: Lees het blad Van
jaarcirkel tot gradenboog = https://www.cielen.eu/van-jaarcirkel-tot-gradenboog.pdf Blad 7: Teken
verschillende hoeken van opgegeven graden kriskras op het blad. Schrijf de
grootte van elke hoek erbij. De opgegeven hoeken mogen scherp, recht en stomp
zijn. Gebruik bij voorkeur ronde getallen die gemakkelijk te herkennen zijn
op de gradenboog. Bv. 30°, 45°, 120°
enz.
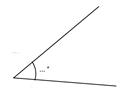
Blad 8: Teken kriskras
over het blad een aantal scherpe hoeken. Teken eerst de hoeken en meet dan
(zo nauwkeurig mogelijk) de hoek. Schrijf in elke hoek de maat ervan. Blad 9: Teken kriskras
over het blad een aantal stompe hoeken. Schrijf in elke hoek de maat ervan. Teken
eerst de hoeken en meet ze dan zo nauwkeurig mogelijk.
Blad 10: Teken kriskras over het
blad een aantal rechte hoeken. Schrijf in elke hoek de maat ervan. Uitleg
vind je op https://www.cielen.eu/rechte-hoeken-tekenen-uitleg.pdf
Blad 11: Gebruik een
winkelhaak (of maak er een in hout) en zoek daarmee in huis zo veel mogelijk
rechte hoeken (Bv. muren, tafels enz. ). Maak enkele schetsen van die hoeken.
VANAF
HIER gaan alle lijnen die je met het harde potlood tekent dóór de snijpunten
en hoekpunten. Ze stoppen NOOIT in een hoek of bij een punt, maar gaan er
ALTIJD door. Bij de afwerking in kleur stop je wel bij hoeken en snijpunten,
maar de potloodlijnen die verdergaan mag je blijven zien. Zie ook:
https://www.cielen.eu/meetkunde-5e-klas-zeshoek-zesster-regelmatige-vlakke-figuren.pdf. (De opgaven op de pagina van de site komen hieronder ook
aan bod). Blad 12: Zet een stip op
het midden van een blad (trek de diagonalen en gom die weg zodra je het
middelpunt hebt aangestipt). Teken vanuit dit middelpunt een cirkel met een
straal van naar keuze 4cm of 4,5 cm of 5 cm. Met dezelfde passeropening teken
je op elk nieuw snijpunt een cirkel op de cirkelomtrek. Werk mooi af in
kleur.
Blad 13: Idem als de
vorige opgave, maar verbind nu de snijpunten van de bogen binnen de middelste
cirkel met rechte lijnen. Werk mooi af in kleur.
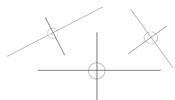
Blad 14: Zet een stip op
het midden van het blad (eerst diagonalen tekenen en daarna uitgommen). Teken
een cirkel met straal van 3 of 3,5 of 4 cm. Teken een middellijn. Maak de
passeropening groter. Teken op elk snijpunt van middellijn en cirkelomtrek
een cirkel. Gom een deel van die drie cirkels uit, maar zorg dat de
snijpunten van de bogen onder en boven zichtbaar blijven. Trek een rechte
lijn door de snijpunten. Meet de hoeken waar de twee rechte lijnen elkaar
snijden. Hoe heten die hoeken? Hoeveel graden zijn de hoeken tezamen?
Blad 15: Idem als 14. Zet een stip op het
midden van het blad. Teken een rechte lijn die door de stip gaat. Teken een
cirkel (r = 3 of 3,5 of 4 cm – kies een andere maat dan blad 14) met de stip
als middelpunt. Gom de cirkel uit, behalve de snijpunten met de lijn. Maak de
passeropening groter en teken vanuit elk snijpunt een cirkel. Gom de cirkels
uit, behalve de snijpunten van de bogen. Trek een lijn door de snijpunten.
Meet de hoeken. De som van de hoeken is … ° Blad 16: Loodlijnen
tekenen. Idem als 14 en 15, maar de cirkels niet meer volledig tekenen,
alleen de boogjes bij de snijpunten. Teken een rechte lijn ergens
op het blad. Zet een stip op het midden van de lijn. Neem de passer en open
hem tot hij iets kleiner is dan de helft van de rechte lijn. Zet de
passerpunt op de middenstip en teken een boogje links van de stip en een
boogje rechts van de stip. Maak de passeropening iets groter en teken twee
boogjes boven en twee boogjes onder het middelpunt van de rechte lijn: dit
zijn de nieuwe snijpunten. Trek er een rechte lijn door. Nu heb je twee
lijnen die loodrecht op elkaar staan. Maak nog enkele gelijkaardige
tekeningen op het blad, maar groter en/of kleiner dan de eerste figuur. Het woord loodlijn uitleggen.
Als je een stuk lood aan een touw naar beneden laat hangen (zoals metselaars
dat doen), dan vormt het touw een loodlijn = loodrechte in de richting van
het middelpunt van de aarde. Een loodlijn staat loodrecht op een horizontale
lijn en heet daarom ook verticale lijn of verticale. Vanaf nu kun je spreken van rechte
= rechte lijn horizontale
= horizontale lijnen (van links naar rechts of andersom) verticale
= verticale lijnen (van boven naar beneden of andersom) loodlijn = lijn die loodrecht staat op een andere
lijn en daarmee hoeken van 90° vormt (rechte hoeken). Blad 17: Loodlijnen
tekenen met de tekendriehoek. Dit is de eenvoudigste manier om loodlijnen te
tekenen, maar ook de minst nauwkeurige. Teken een willekeurige rechte. Leg
een lat naast de rechte en laat de tekendriehoek (geodriehoek) erover
schuiven. Alle lijnen die je langs de rechte zijde van de tekendriehoek kunt
tekenen, staan loodrecht op de rechte. Teken verschillende rechten met daarop
loodlijnen. Blad 18: Vierkant met
geodriehoek. Teken een rechte en meet er een stuk van 7 cm op af (zet 2 stippen
op 7 cm van elkaar). Leg de lat ernaast en teken op elke stip een loodlijn
(maak ze langer dan 7 cm). Meet op elke loodlijn 7 cm af. Verbind de 2 punten
met een nieuwe rechte en het vierkant is klaar. Teken verschillende
vierkanten op het blad. De vierkanten mogen door elkaar gaan en elk vierkant
heeft een andere maat. Schrijf in elk vierkant hoe lang een zijde is en hoe
lang de omtrek is. Hoe bereken je de omtrek? Blad 19: idem als 18,
maar gebruik nu de passer om de zijde van het vierkant af te meten op de
loodlijnen (= je maakt de passeropening net zo groot als de zijde van het
vierkant). Teken verschillende vierkanten. Zet erin Z = … cm en Om = …. cm. Blad 20: Zeshoek en zesster met passer en lat. Teken
de diagonalen van het blad en zet een stip in het midden. Gom de diagonalen
uit. Zet
passerpunt op de middenstip. Open de passer tot 10 cm. Teken de cirkel. Laat
de passeropening zoals hij is en teken ergens op de cirkelomtrek een cirkel. Op
de snijpunten van 1e cirkel en 2e cirkel teken je weer cirkels. Gom
de cirkels uit en laat alleen de snijpunten (boogjes) op de 1e cirkel staan. Verbind
de punten op de cirkelomtrek met rechte lijnen. Zie:
https://www.cielen.eu/hoeken-60-graden-tekenen-zesster-zeshoek.pdf Afwerken
in kleur met dubbele lijnen + vlechten. Blad 21: Zeshoek en zesster met lat en gradenboog. (alternatieve manier
om zeshoek en zesster te tekenen) Blad 22: Driehoeken in
zeshoek-zesster? Zie: https://www.cielen.eu/zeshoek-zesster-tekenen-potlood-passer-lat-uitleg.pdf Teken een
zeshoek + zesster. Geef de randen van elke driehoek die je in de figuur ziet
een kleur. Alle driehoeken die even groot zijn krijgen dezelfde kleur. Hoeveel driehoeken zie je in de figuur? Blad 23: Rechthoeken
ontdekken in zeshoek-zesster. Zie: https://www.cielen.eu/rechthoeken-ontdekken-in-zeshoek-zesster-uitleg.pdf
Blad 24: Ruiten ontdekken in
zeshoek-zesster. Zie: https://www.cielen.eu/zeshoek-zesster-ruiten.pdf
(bekijk dit pas NA het tekenen en nadat je zelf ruiten gevonden
hebt. Blad 25: Parallellogrammen
ontdekken in zeshoek-zesster. Blad 26: Trapeziums ontdekken
in zeshoek-zesster. Blad 27: Van zeshoek-zesster tot vierkant tekenen Zie: https://www.cielen.eu/zeshoek-zesster-vierkant-uitleg.pdf Blad 28: De oppervlakte van
het vierkant. Teken
een vierkant met z
(zijde) = 10 cm. Gebruik lat, geodriehoek en passer of lat, gradenboog en
passer. Verdeel elke zijde in centimeters en verbind die met
rechte lijnen zodat het vierkant helemaal gevuld is met kleinere vierkanten.
Hoeveel vierkanten tel je op de oppervlakte van het grote vierkant? Hoe noteer je dit? = vierkantjes van 1cm x 1 cm = 1 cm².
Elk vierkantje is 1 cm² groot. In het hele vierkant kunnen 100 kleine
vierkantjes of 10 cm x 10 cm = 100 cm², uitgesproken als vierkante
centimeter. De kleine ² verwijst naar de vermenigvuldiging waarin je tweemaal
het woord cm hebt gebruikt: cm x cm = cm². Teken verschillende vierkanten (van bv. z = 2 cm, Z = 3 cm enz.) en verdeel ze in vierkantjes van
1 cm². De vierkanten mogen door elkaar gaan. Wat is de oppervlakte van elk vierkant? Wat is de oppervlakte van een vierkant van z = 1 cm? Zet de getallen van de oppervlakte van klein naar groot.
Welke getallenrij is dit?
Blad 30: Teken verschillende
vierkanten door elkaar. Geef elk vierkant een andere kleur. Schrijf in
elk vierkant het volgende: Z
= … cm (z =
zijde) Om
= … cm (om = omtrek) Op
= … cm² (op = oppervlakte) Blad 31: Teken de volgende
vierkanten en schrijf de naam, de z, de om en de op
in elk vierkant Vierkant
“Ekeren” heeft zijden van 3,5 cm Vierkant
“Sint-Mariaburg” heeft zijden van 7,7 cm Vierkant
“Brasschaat” heeft zijden van 4,9 cm Vierkant
“Kapellen” heeft zijden van 1,8 cm Vierkant
“Boon” heeft zijden van 1,52 dm Vierkant
“Antwerpen” heeft zijden van 6 mm (= … cm) Vierkant
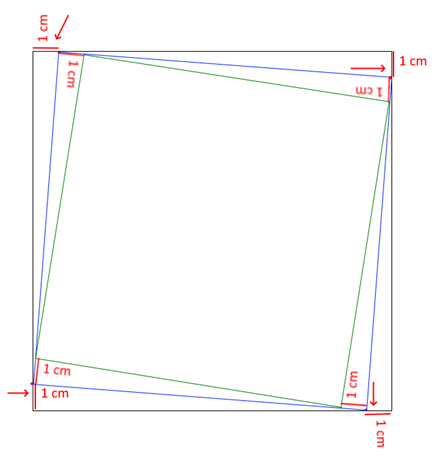
“Luchtbal” heeft zijden van 10,10 cm Blad 32: Het vierkant beweegt.
Teken
een vierkant met z = 15 cm Meet 1 cm af vanaf elke hoek en ga daarvoor met de klok
mee: hoek bovenaan rechts, meet 1 cm naar beneden, hoek onderaan rechts 1 cm
naar links, onderaan links 1 cm naar omhoog, bovenaan links = 1 cm naar
rechts. Verbind de vier punten: je krijgt een vierkant dat een beetje schuin
staat. Op het schuine vierkant doe je hetzelfde als op het
eerste vierkant; vanaf elke hoek 1 cm afmeten en met de klok meegaan. Je krijgt
een vierkant dat nog wat schuiner staat. Op het nieuwe schuine vierkant doe je weer hetzelfde. Op elk nieuw vierkant doe je hetzelfde tot het niet meer
kan. Werk de omtrek van de vierkanten af met zwarte stift of
geef elk vierkant een eigen kleur.
Blad 33: Zoek vierkanten in
huis (of ergens anders). Zoek
vierkanten en maak er een lijst van (bv. tegel in de keuken: z = … cm, om = … cm, op = … cm²). Meet
van elk vierkant de zijde. Bereken
van elk vierkant de omtrek en oppervlakte.
Blad 34: De eigenschappen van
het vierkant. Teken
een vierkant met z = 10 cm. Meet
de hoeken Teken
de diagonalen Meet
de hoeken in het midden op het snijpunt van de diagonalen Meet
de hoeken die de diagonalen maken in de hoeken van het vierkant NOTEER:
De
4 zijden zijn even lang De
4 zijden staan loodrecht op elkaar De
4 hoeken zijn recht = 90°. De 4 hoeken samen = 360° (= 4 x 90°) De
4 hoeken op het snijpunt van de diagonalen zijn recht = 90° (4 x 90° = 360°) De
diagonalen vormen met de hoeken van het vierkant hoeken van 45° De
2 diagonalen zijn even lang De
diagonalen snijden elkaar in het midden van het vierkant. De
omtrek (om) = z x 4 De
oppervlakte (op) = z x z
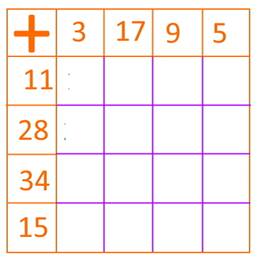
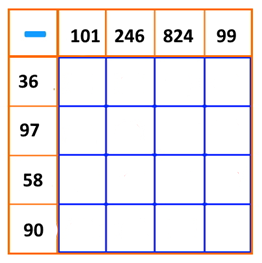
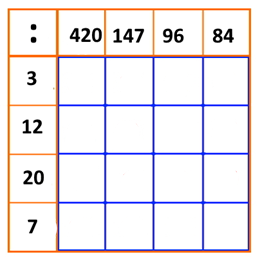
= z² Aanvullende opdrachten: Maak een vierkant van 1 m² en verdeel in dm². Hoeveel dm² is dat? Maak een vierkant van 1 dm² en verdeel in cm². Maak er nog enkele, knip uit en bedek er de m² mee. Maak een vierkant van 1 cm² en verdeel in mm². Maak er nog enkele (zonder verdeling in mm²) en bedek er een dm² mee. Hoeveel m² kunnen er op de vloer van een kamer, klas, gang, tuin, schoolplein, enz.? Zoek in de omgeving een plek die +/- 1 dam² (100 vierkante meter) groot is of teken er in het zand een vierkant van 1 dam² (z = 10 m). Zoek in de omgeving een vierkant van 1hm² (100 m x 100m). (bv. 2 voetbalvelden naast elkaar). Zoek in de omgeving een vierkant van +/- 1 km², zodat je een beeld krijgt van hoe groot een km² is. Dit sluit aan bij de lessen aardrijkskunde waar bevolkingscijfers in km² uitgedrukt worden, ook de grootte van gemeenten en landen wordt meestal in km² gegeven. Blad 35: Plusvierkant, minvierkant,
tafelvierkant, deelvierkant Teken deze vierkanten en vul ze in. Z van
elk vierkant = 10 cm.
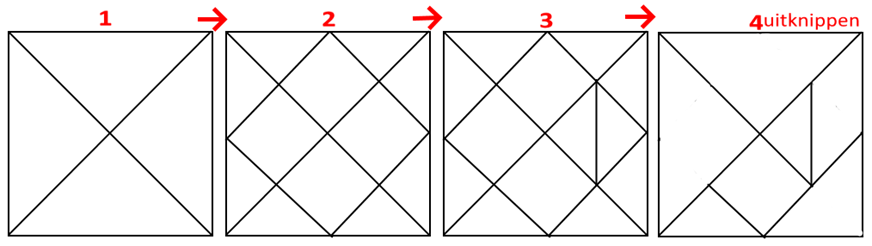
Blad 36: Het tangram Teken het vierkant (z = 10 cm
of meer of minder naar keuze) stevig papier of plak het blad op karton.
Verdeel het zoals op de tekening en knip uit. Leg met de stukken enkele
figuren uit de afbeelding hieronder. .
Zie ook: https://www.cielen.eu/meetkunde-6e-klas-tangram-DM-2013.pdf Klik op de
afbeelding voor opgave + oplossing Blad 37: De QR-code De QR-codes staan op dit blad. Meet de zijde van elk vierkant. Schrijf de maat bij één
van de zijden. Bereken omtrek en oppervlakte. Schrijf om en op
bij elk vierkant. Als alles genoteerd is, scan je de QR-codes en zie je telkens een vraag. Schrijf het antwoord onder de QR-code. Klik op de afbeelding links voor de opgave op A4-formaat. De oplossingen van de vragen vind je hier. Blad 38:
Deelbaarheidsvierkant Zijn de getallen in de bovenste rij deelbaar door de getallen in de linker kolom? Heb je niet alle deelbaarheidsregels geleerd, kijk dan
op: https://www.cielen.eu/regels-deelbaarheid-GGD-KGV.pdf Vul in met J of N. Weet je het niet, dan vul je in met X. Teken het vierkant met z = 20
cm. Verdeel het vierkant in 100 vakjes. Omtrek = Oppervlakte =
Blad 39: Statisch en
dynamisch vierkant Teken twee vierkanten met z = 6
cm. Verdeel de zijden in
stukjes van 3 mm en vul het vierkant met vierkantjes (z = 3 mm). In één vierkant teken je de lijnen langs een lat en kleur
je de vakjes in met afwisselend wit en zwart (zoals dambord). Het andere vierkant trek je gebogen lijnen, die nu eens
dicht bij elkaar komen, dan weer ver van elkaar gaan. Kleur deze vakjes ook
in met wit en zwart afwisselend.
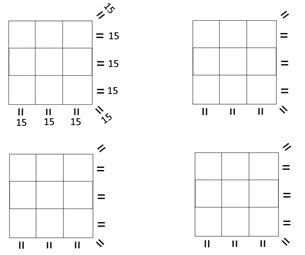
Blad 40: Tovervierkanten
(magische vierkanten) Verdeel het blad in 4. Teken in elk kwart een vierkant met z
= 6 cm Verdeel elk vierkant in 9 vierkantjes In het eerste vierkant vul je de getallen 1 tot en met 9
in op zo’n manier dat de som van elke rij en elke kolom en elke diagonaal
gelijk is aan 15. In het tweede vierkant vul je de getallen van de tafel
van 2 in: 2 – 4 – 6 -------------- 18. De uitkomst van elke rij, kolom en
diagonalen is dan gelijk aan ….? In het derde vierkant de getallen van de tafel van 3: 3 –
6 -9 ------------27. De uitkomst van elke rij, kolom en diagonalen is dan
gelijk aan ….? In het vierde vierkant de getallen van de tafel van 4: 4
– 8 – 12 - ------- 36. De uitkomst van elke rij, kolom en diagonalen is dan
gelijk aan ….?
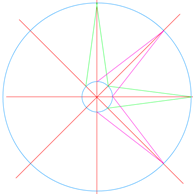
Blad 41: De windroos Zet
een stip op het midden van het blad. Laat
alle lijnen die je tekent doorlopen tot de rand van het blad (maar zacht,
zodat je ze nog kunt uitgommen Teken
een rechte lijn (horizontaal) die evenwijdig loopt aan de rand van het blad. Teken
een loodlijn (verticaal) midden op de horizontale lijn. Verdeel
elke hoek in de helft (gebruik een gradenboog). Zet
de passerpunt op de middenstip en trek een cirkel met straal = 6 cm (5cm of 7
of 8 of 9 cm is ook oké). Teken
nog een cirkel met straal = 2 cm. Werk
bij zoals op de tekening hieronder:
Als
de tekening af is, zet er dan de windstreken bij; het noorden bovenaan. Voor
de opdrachten 42 tot en met 47 heb je tekenpapier nodig (dikker dan de
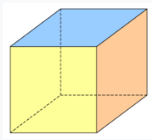
meetkundebladen), bv. 150 gr en een lijmpistool. Blad 42: De hexaëder
(regelmatig zesvlak) = 2e platonisch lichaam Zie: https://www.cielen.eu/meetkunde-vijfde-klas-hexaeder.pdf Maak
deze opdracht 2 keer. 1
blad blijft als meetkundige tekening. 1
blad dient om uit te snijden en in elkaar te steken.
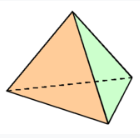
Blad 43: De tetraëder
(regelmatig viervlak) = 1e platonisch lichaam Zie:
https://www.cielen.eu/tetraeder-uitleg.pdf Maak deze
opdracht 2 keer. 1
blad blijft als meetkundige tekening. 1
blad dient om uit te snijden en in elkaar te steken.
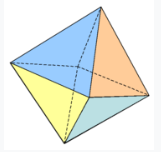
Blad 44: octaëder (regelmatig
achtvlak) = 3e platonisch lichaam Zie: https://www.cielen.eu/wiskunde-octaeder-uitleg.pdf Maak deze
opdracht 2 keer. 1
blad blijft als meetkundige tekening. 1
blad dient om uit te snijden en in elkaar te steken.
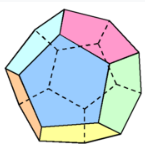
Blad 45: de dodecaëder
(regelmatig twaalfvlak) = 4e platonisch lichaam Zie: https://www.cielen.eu/meetkunde-vijfde-klas-dodecaeder-constructie.pdf Maak deze
opdracht 2 keer. 1
blad blijft als meetkundige tekening. 1
blad dient om uit te snijden en in elkaar te steken.
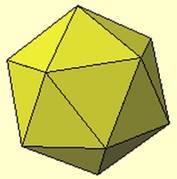
Blad 46: De icosaëder
(regelmatig twintigvlak) = 5e platonisch lichaam Zie: https://www.cielen.eu/meetkunde-5e-klas-icosaeder.pdf of: https://www.cielen.eu/icosaeder-bouwplan.pdf Maak deze
opdracht 2 keer. 1
blad blijft als meetkundige tekening. 1
blad dient om uit te snijden en in elkaar te steken.
Blad 47: De caleidocyclus (Escher) https://nl.wikipedia.org/wiki/Maurits_Cornelis_Escher Zie: https://www.cielen.eu/meetkunde-vijfde-klas-caleidocyclus.pdf
Maak deze opdracht 2 keer. 1
blad blijft als meetkundige tekening. 1
blad dient om uit te snijden en in elkaar te steken.
MOGELIJKE EXTRA OPGAVEN Blad 48: Zeshoek en zesster tekenen met passer, gradenboog en lat. = https://www.cielen.eu/hoeken-60-graden-tekenen-zesster-zeshoek.pdf Blad 49: Zeshoek en zesster tekenen met passer en lat = https://www.cielen.eu/zeshoek-zesster-tekenen-potlood-passer-lat-uitleg.pdf Blad 50: Vijfhoek en
vijfster tekenen met passer, gradenboog en lat. = https://www.cielen.eu/hoeken-72-graden-tekenen-vijfhoek-vijfster-uitleg.pdf Blad 51: Van zesster tot vijfster = https://www.cielen.eu/van-zesster-tot-vijfster-uitleg.pdf IN DE ZESDE KLAS ga je voort
met VLAKKE MEETKUNDE: vierkant, rechthoek, parallellogram, ruit, vlieger, driehoek,
trapezium, cirkel en daarna de VOLUMES: kubus en alle soorten parallellepipeda
(zoals balk, cilinder en andere), piramide, kegel, bol. Zie: meetkunde-6e-klas-programma (nog niet beschikbaar op 2020-10-25, je vind wel info op https://cielen.eu/vakken/wiskunde/meetkunde.html) |
|
https://www.cielen.eu |